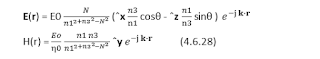Chapter 4 : Propagation In Birefringent Media
Propagation In Birefringent Media
optikal
aktif atau kiral Mediasecara melingkar birefringent. Contohnya
adalah larutan gula, protein, lipid, asam nukleat, asam amino, DNA, vitamin,
hormon, dan hampir semua zat alami lainnya. Dalam media seperti itu, gelombang
terpolarisasi sirkuler tidak mengalami perubahan, dengan polarisasi kiri dan
kanan melingkar pada kecepatan yang berbeda. Perbedaan ini menyebabkan
gelombang terpolarisasi linier untuk memiliki pesawat polarisasi berputar
ketika mereka menyebar-efek yang dikenal sebagai rotasi optik alami.
Efek yang serupa tetapi
tidak identik — rotasi Faraday —mengambil tempat digyroelecric media,
yang merupakan material isotropik biasa (kaca, air, konduktor, plasma) yang
mengalami medan magnet eksternal konstan yang memecah isotropinya. Gyromagnetic
Media, seperti ferrit yang mengalami medan magnet, juga menjadi bundar
birefringent. Kami membahas semua empat kasus birefringent (linear, kiral,
gyroelectric, dan gyromagnetic) dan jenis hubungan konstitutif yang mengarah
kebirefringent yang sesuai
perilaku.
Gyrotropic Media
Gyrotropic†
media media yang isotropik di hadapan konstan eksternal medan magnet fi .
Sebuah media gyroelectric (difrekuensi) ωmemiliki hubungan konstitutif:
Fig. 4.2.1 Linearly and circularly birefringent retarders.
Gyrotropic Media
Gyrotropic†
media media yang isotropik di hadapan konstan eksternal medan magnet fi .
Sebuah media gyroelectric (difrekuensi) ωmemiliki hubungan konstitutif:
impedansi sirkular terkait η±
Ini
memenuhi persamaan yang dipisahkan:

Dengan demikian, bidang dasar melingkar lengkap E±(z) adalah:
Sekarang,
komponen sirkular E + (z) menjalar ke depan dan ke belakang dengan bilangan gelombang k+ yang sama,
sementara E- menyebar
dengan k_. Rotasi bidang polarisasi
disebut sebagai rotasi Faraday. Jika
propagasi adalah di negatif z-arah, maka peran k+ dan k_ tetap
tidak berubah sehingga sudut rotasi masih sama seperti yang dari Persamaan.
(4.4.8).
Jika gelombang
lurus linear bergerak maju dengan jarak l,
tercermin, dan bergerak kembali ke titik awal, total sudut rotasi akan menjadi
dua kali lipat dari perjalanan tunggal, yaitu, 2ϕ = (k+ - k-)l.
Casing
gyromagnetik pada dasarnya identik dengan gyroelectric. Persamaan. (4.4.5)
hingga (4.4.8) tetap sama, tetapi dengan bilangan gelombang sirkit dan
impedansi yang ditentukan oleh:
4.5
Linear dan Edaran Dichroism
Dichroic polarizers, seperti
polaroid, adalah bahan birefringent linear yang memiliki
koefisien atenuasi yang berbeda sepanjang dua arah polarisasi. Untuk materi lossy, solusi diberikan dalam Persamaan. (4.5.1) dimodifikasi sebagai berikut:
koefisien atenuasi yang berbeda sepanjang dua arah polarisasi. Untuk materi lossy, solusi diberikan dalam Persamaan. (4.5.1) dimodifikasi sebagai berikut:
Ex = Ae-jk
1z = Ae – α1z e –jβ11z , k1= ω β1 - j α1 (4.5.1)
Ex
= Be-jk2z
= Be – α2z e –jβ11z , k2= ω
β2 - j α2
dimana α1, α2 adalah koefisien
atenuasi. Melewati panjang l dari seperti itu
material, polarisasi awal dan output akan menjadi sebagai berikut:
material, polarisasi awal dan output akan menjadi sebagai berikut:
E(0) = ẍA + ẏB
E(1) = ẍ Ae-jk1l + ẏ Be-jk2l
= (ẍ Ae - α1
+ ẏ Be – α2l e jϕ ) e-jβl (4.5.2)
Sebuah
polarizer linier ideal akan memiliki a1 = 1 dan a2 = 0, sesuai dengan α1 = 0
dan α2 = . Nilai-nilai khas dari redaman untuk tersedia secara komersial
polaroid yangadalah urutan a1 = 0,9 dan a2 = 10-2, atau 0,9 dB dan 40 dB, masing-masing.
Media kiral dapat menunjukkan dichroism sirkular [722,735], di mana jumlah gelombang lingkar menjadi kompleks, k± = β± - jα±. Persamaan (4.3.11) dibaca sekarang:
polaroid yangadalah urutan a1 = 0,9 dan a2 = 10-2, atau 0,9 dB dan 40 dB, masing-masing.
Media kiral dapat menunjukkan dichroism sirkular [722,735], di mana jumlah gelombang lingkar menjadi kompleks, k± = β± - jα±. Persamaan (4.3.11) dibaca sekarang:
E(l) = ẻ +A+ e-jk+l + ẻ-A- e-jk-l
= [ẻ +A+e-j (k+ -k-) l /2 + ẻ -A-ej (k+ -k-) l /2 ] e-j (k++k-) l /2
= [ẻ +A+e-ψ-jφ + ẻ -A-eψ+jφ] e-j (k++k-) l /2 (4.5.3)
= [ẻ +A+e-ψ-jφ + ẻ -A-eψ+jφ] e-j (k++k-) l /2 (4.5.3)
dimana kami mendefinisikan sudut
rotasi kompleks:
φ - jψ =  (k+ - k-) l =
(k+ - k-) l =  (β+ - β-) l -
j
(β+ - β-) l -
j
 (α+ - α-)l
(4.5.4)
(α+ - α-)l
(4.5.4)
Kembali
ke basis linier seperti pada Persamaan. (4.5.5), kami memperoleh:
E(0)= [ẍAx + ẏ Ay]
E(l) = [ẍ`A`x + ẏ A`y] e-j (k++k-) l /2 (4.5.5)
E(l) = [ẍ`A`x + ẏ A`y] e-j (k++k-) l /2 (4.5.5)
dimana {ẍ`, ẏEQ`} adalah
yang dirotasi (oleh φvektor unit persamaan). (4.3.13), dan
A`x = Ax
cosh
ψ
-
jAy
sinh
ψ
A`y = Ay cosh ψ + jAx sinh ψ (4.5.6)
A`y = Ay cosh ψ + jAx sinh ψ (4.5.6)
Karena amplitudo A x, A y sekarang
bernilai kompleks, polarisasi yang dihasilkan
akan elips.
akan elips.
4.6 Perbanyakan Miring di
Birefringent Media
Aplikasi
termasuk cermin polimer birefringent multilayer yang baru saja diproduksi (oleh
3M, Inc.) yang memiliki sifat optik yang luar biasa dan tidak biasa, secara
kolektif
disebut sebagai optik birefringent raksasa (GBO) [698].
disebut sebagai optik birefringent raksasa (GBO) [698].
4.6. Propagasi Oblique di Birefringent Media
Kami
ingat dari Sec. 2.10 bahwa merambat gelombang bidang seragam dalam lossless
isotropik
dielektrik dalam arah vektor gelombang k diberikan oleh:
E(r)=
E e-j k·r
, H(r)= H e-j
k·r , with ḱ· E = 0 , H =  ḱ × E
(4.6.1)
ḱ × E
(4.6.1)
dimana n adalah indeks refraktif dari medium n = n = η0 impedansi ruang bebas,
dan ḱ unit-vektor ke arah k, sehingga,
k = k ḱ, k = |k| = ω= nk0 , k0 = (4.6.2)
dan k0 adalah bilangan gelombang ruang bebas. Jadi, E, H,
ḱ membentuk sistem tangan kanan.
Secara
khusus, mengikuti notasi Gambar. 2.10.1, jika k dipilih untuk terletak pada bidang xz
pada sudut θ dari sumbu z, yaitu, ḱ = ẍsin θ + ẑ cos θ, maka akan ada dua solusi polarisasi independen: TM, paralel, atau p-polarisasi, dan TE, tegak lurus, atau s-polarisasi, dengan bidang yang diberikan oleh
pada sudut θ dari sumbu z, yaitu, ḱ = ẍsin θ + ẑ cos θ, maka akan ada dua solusi polarisasi independen: TM, paralel, atau p-polarisasi, dan TE, tegak lurus, atau s-polarisasi, dengan bidang yang diberikan oleh
(TM, p-polarization): E =
E0(ẍ cos θ - ẑ sin θ) , H =
 E0 ẏ
E0 ẏ
(TE, s-polarization): E =
E0 ẏ, H =  E0 (-ẍcos θ + ẑsin
θ) (4.6.3)
E0 (-ẍcos θ + ẑsin
θ) (4.6.3)
dimana,
baik dalam kasus TE dan TM, propagasi faktor fasee-jk·r adalah:
e-jk
· r = e-j(kzz+kxx) = e-jk0n (z cos θ + x sin θ) (4.6.4)
Antarmuka
dielektrik diambil menjadi bidang xy dan bidang xz menjadi
bidang insiden. Dalam media birefringent, propagasi gelombang bidang seragam
vektor gelombang k jauh lebih sulit untuk dijelaskan. Sebagai contoh, arah
vektor Poynting tidak menuju k, medan listrik E tidak ortogonal terhadap k,sederhana
hubungan dispersik = nω / c0 tidak valid, dan seterusnya.
bidang insiden. Dalam media birefringent, propagasi gelombang bidang seragam
vektor gelombang k jauh lebih sulit untuk dijelaskan. Sebagai contoh, arah
vektor Poynting tidak menuju k, medan listrik E tidak ortogonal terhadap k,sederhana
hubungan dispersik = nω / c0 tidak valid, dan seterusnya.
Hubungan
konstitutif diasumsikan menjadi B =
μ0H dan permitivitas
diagonal
tensor untuk D. ε1,ε2,ε3 menjadi nilai-nilai permitivitas sepanjang tiga sumbu pokok dan
menentukan indeks bias yang sesuai ni = , i = 1, 2, 3. Kemudian, D -E
hubungan menjadi:
tensor untuk D. ε1,ε2,ε3 menjadi nilai-nilai permitivitas sepanjang tiga sumbu pokok dan
menentukan indeks bias yang sesuai ni = , i = 1, 2, 3. Kemudian, D -E
hubungan menjadi:
Gambar 4.6.1 Gelombang
bidang seragam dalam medium birefringent.
Untuk
media biaksial, tiga ni semuanya berbeda. Untuk media uniaksial, kita mengambil
sumbu xy menjadi biasa, dengan n1 = n2 = tidak, dan sumbu-z menjadi luar biasa, dengan
n3 = ne. † Vektor gelombang k dapat diselesaikan sepanjang arah z dan x sebagai berikut:
sumbu xy menjadi biasa, dengan n1 = n2 = tidak, dan sumbu-z menjadi luar biasa, dengan
n3 = ne. † Vektor gelombang k dapat diselesaikan sepanjang arah z dan x sebagai berikut:
k = k ḱ = k (ẍsinθ + ẑcos θ) = ẍ kx +ẑkz (4.6.6)
Hubungan
ω-k ditentukan dari solusi persamaan
Maxwell. Dengan
analogi dengan kasus isotropik yang memiliki k = nk0 = nω / c0, kita dapat mendefinisikan efektif
indeks bias N sehingga:
analogi dengan kasus isotropik yang memiliki k = nk0 = nω / c0, kita dapat mendefinisikan efektif
indeks bias N sehingga:
Kita
akan lihat dalam Persamaan. (4.6.2) dengan menyelesaikan persamaan Maxwell
bahwa N bergantung pada polarisasi yang dipilih (menurut Gambar 4.6.1) dan pada
arah vektor gelombang θ:
Untuk kasus TM, kita dapat menulis ulang hubungan N-θ dalam bentuk:
Mengalikan dengan k2 dan menggunakan k0 = k / N, dan kx = k sin θ, kz =
k cos θ, kita memperoleh
ω -k hubungan untuk kasus TM:
ω -k hubungan untuk kasus TM:
4.6. Oblique Propagation di Media Birefringent
Dengan demikian, mode TE menyebar
seolah-olah mediumnya isotropik dengan indeks n = n2,
sedangkan mode TM menyebar dengan cara yang lebih rumit.
sedangkan mode TM menyebar dengan cara yang lebih rumit.
Untuk mode TM, kecepatan grup
tidak sepanjang k. Secara umum,
kecepatan grup
tergantung pada hubungan ω-k dan dihitung sebagai v = ∂ω / ∂k. Dari Persamaan. (4.6.10), kita
menemukan komponen x dan z:
tergantung pada hubungan ω-k dan dihitung sebagai v = ∂ω / ∂k. Dari Persamaan. (4.6.10), kita
menemukan komponen x dan z:
Vektor kecepatan v tidak
sejajar dengan k. Sudut θ ¯ bahwa v bentuk-bentukdengan sumbu-z
diberikan oleh tan θ ¯ = vx / vz. Ini mengikuti dari (4.6.12) bahwa:
diberikan oleh tan θ ¯ = vx / vz. Ini mengikuti dari (4.6.12) bahwa:
Poynting vektor P dan densitas energi w sebagai v = P / w. Jadi, v dan P memilikisama
arah yang. Selain itu, dengan medan listrik yang ortogonal terhadap vektor Poynting,
sudut θ ¯ juga sama dengan sudut bentuk E-field dengan sumbu x.
Gambar
4.6.2 Arah kecepatan kelompok, vektor Poynting, vektor gelombang, dan medan
listrik.
Selanjutnya, kita memperoleh Persamaan. (4.6.8) untuk N dan pecahkan komponen lapangan dalam kasus TM dan TE. Kami mencari solusi propagasi persamaan Maxwell dari tipe
E(r) = E ej k·r dan H(r) = H ej k·r. Mengganti operator gradien dengan ∇ → jk dan
membatalkan beberapa faktor j, persamaan Maxwell mengambil bentuk:
Dua persamaan terakhir yang tersirat oleh dua yang pertama,
seperti yang dapat dilihat oleh menghiasi kedua sisi dua yang pertama dengan k. Mengganti k = k k ˆ = Nk0k ˆ, di mana N masih harus ditentukan,
kita dapat menyelesaikan hukum Faraday untuk H dalam hal E :
dimana kita menggunakan η0 = c0μ0. Kemudian, hukum Amp`s memberi:
dimana kami menggunakan c0η0 = 1 / ϵ0. Kuantitas k ˆ × (E×k ˆ) dikenal sebagai
komponen
E yang melintang ke vektor unit propagasi k ˆ. Dengan menggunakan identitas vektor BAC-CAB,
E yang melintang ke vektor unit propagasi k ˆ. Dengan menggunakan identitas vektor BAC-CAB,
kita memiliki k ˆ × (E × k ˆ) = E - k ˆ (k ˆ · E). Menata ulang
istilah, kita memperoleh:
Untuk mendapatkan solusi TE dan
TM, kami berasumsi awalnya bahwa E memiliki
semua tiga komponen dan menulis ulang Persamaan. (4.6.16) komponen-bijaksana.
Menggunakan Persamaan. (4.6.5) dan mencatat bahwa k ˆ · E = Ex cos θ + Ez
cos θ, kita memperoleh sistem linear homogen:
4.6. Oblique Propagation di Birefringent Media di
mana faktor fase propagasi TE adalah:
dimana faktor fase propagasi TE adalah:
Menggunakan identitas sin2 θ + cos2 θ = 1, kita dapat menulis ulang
Persamaan. (4.6.20) dalam bentuk matriks:
Mengatur determinan matriks koefisien ke nol, kita memperoleh
kondisi yang diinginkan pada N agar solusi non-nol Ex, Ez ada:
Ini dapat dipecahkan untuk N2 untuk memberikan Persamaan. (4.6.9).
Dari itu, kita juga dapat memperoleh berikut hubungan,
yang akan terbukti berguna dalam menerapkan hukum Snel di media birefringent:
Dengan bantuan hubungan yang diberikan dalam Soal 4.16, solusi
dari sistem homogen (4.6.20) ditemukan menjadi, hingga konstanta proporsionalitas:
Konstanta A dapat dinyatakan dalam besaran total bidang E0 =
|E| = | Ex | 2 + | Ez | 2. Menggunakan hubungan (4.7.11), kita menemukan (dengan asumsi A> 0):
|E| = | Ex | 2 + | Ez | 2. Menggunakan hubungan (4.7.11), kita menemukan (dengan asumsi A> 0):
Medan magnet H juga
dapat diekspresikan dalam bentuk konstanta A. Kita memiliki:
faktor fase propagasi TM adalah:
= (z cosθ+x sin θ)
(TM propagation factor)
Solusinya telah dimasukkan ke dalam bentuk yang
menunjukkan batas yang tepat pada θ = 0o dan
90o. Ini setuju dengan Persamaan. (4.6.3) dalam kasus
isotropik. Sudut yang E bentuk dengan sumbu x
pada Gambar 4.6.2 diberikan oleh tan ¯θ = −Ez / Ex dan
setuju dengan Persamaan. (4.6.13).
Selanjutnya, kita mendapatkan ekspresi untuk vektor
Poynting dan kerapatan energi. Itu berputar
out-seperti yang umum dalam masalah propagasi dan
waveguide-bahwa energi magnetik
densitas sama dengan listrik. Menggunakan Persamaan.
(4.6.27), kami menemukan:
dan untuk kerapatan energi listrik, magnetik, dan
total:
Vektor P adalah ortogonal terhadap E dan arahnya
adalah θθ yang diberikan oleh Persamaan. (4.6.13), sebagaimana bisa
diverifikasi dengan mengambil rasio tan ¯θ = Px / Pz. Kecepatan transportasi
energi adalah rasio fluks energi ke kerapatan energi — ini sesuai dengan
kecepatan kelompok (4.6.12):
v
=  = Co (ˆx
= Co (ˆx  sinθ + ˆz
sinθ + ˆz  cosθ ) (4.6.31)
cosθ ) (4.6.31)
Polarizer memungkinkan cahaya terpolarisasi linier ke
arah vektor satuan ˆep = ˆx cosθp + ˆy sinθp, seperti ditunjukkan pada Gambar
4.7.1. Output dari polarizer menjalar ke arah z melalui retarder birefringent
linear dengan panjang l, dengan birefringent refractiveindeks n1, n2, dan
retardance φ = (n1 - n2) k0l.
Output E (l) dari sampel birefringent melalui analisis
polarizer linear itu memungkinkan melalui polarisasi melalui vektor satuan ˆea
= ˆx cosθa + ˆy sinθa. Tunjukkan bahwa cahaya Intensitas pada output dari
analisa diberikan oleh:
Ia = | ˆea . · E(l) | = | cosθa cosθp + + ejφ sinθa
sinθp |
Untuk sampel birefringent melingkar yang
memperkenalkan rotasi alami atau Faraday φ =(k + - k−) l / 2, menunjukkan bahwa
intensitas cahaya output adalah:
Ia = | ˆea · E(l) | = cos2(θp −θa −φ)
Propagasi dalam Media Birefringent
4.6 Gelombang
polarisasi linier dengan arah polarisasi pada sudut θ dengan sumbu x berjalan
melalui retarder birefringent melingkar yang
memperkenalkan rotasi optik dengan sudut
φ = (k + - k−) l / 2. Tunjukkan bahwa arah polarisasi
input dan output akan menjadi:
x cosθ + ˆy sinθ → ˆx cos(θ − φ)+ˆy sin(θ − φ)
Konduktor dan plasma menunjukkan perilaku gyroelectric
ketika mereka berada di hadapan suatu
medan magnet luar. Persamaan gerak konduksi elektron
dalam magnet konstan
lapangan adalah m˙v = e (E + v × B) −mαv, dengan
istilah redaman collisional disertakan. Itu
medan magnet dalam arah-z, B = ˆzB0.Asumsikan waktu
ketergantungan dan dekomposisi semua vektor dalam basis melingkar (4.1.1),
misalnya, v = ˆe + v + + ˆe − v− + ˆz vz, menunjukkan bahwa solusi dari persamaan
gerak adalah:di mana ωB = eB0 / m adalah frekuensi siklotron.
Kemudian, tunjukkan bahwa D − E konstitutif.
hubungan mengambil bentuk Persamaan. (4.4.1) dengan:
dimana ω2
p = Ne2 / m_0 adalah frekuensi plasma dan N, jumlah
elektron konduksi
per satuan volume.
Propagasi dalam Media Birefringent
di mana γ adalah rasio gyromagnetic dan τ = 1 / α,
konstanta waktu relaksasi.
Dengan asumsi itu | H | _ H0 dan | M | _ M0, tunjukkan
bahwa versi yang dilinearisasi dari persamaan ini
diperoleh dengan menjaga hanya urutan pertama dalam H
dan M adalah:
di mana ωM = γM0, ωH = γH0, dan χ0 = M0 / H0. Bekerja
dalam basis melingkar (4.1.1), menunjukkan
bahwa solusi dari persamaan ini adalah:
Menulis B = μ0 (H + M), menunjukkan bahwa matriks
permeabilitas memiliki bentuk gipromagnetik
Persamaan. (4.4.2) dengan μ1 ± μ2 = μ ± = μ0 (1 + χ ±)
dan μ3 = μ0. Tunjukkan bahwa bagian nyata dan imajiner dari μ1 diberikan oleh
[750]:
Turunkan ekspresi serupa untuk Re (μ2) dan Im (μ2).
4.14 Gelombang bidang yang seragam, Ee − jk • r dan He
− jk • r, menyebar ke arah vektor unit ˆ k = ˆz_ = ˆz cosθ + ˆz sinθ yang
ditunjukkan pada Gambar 2.10.1 dalam medium gyroelectric dengan hubungan
konstitutif ( 4.4.1) .Menunjukkan bahwa Persamaan. (4.6.14) - (4.6.16) tetap
berlaku asalkan kita mendefinisikan indeks bias efektif N melalui wavevector k
= kˆk, di mana k = Nk0, k0 = ω√μ_0. Bekerja dalam basis circular-polarization
(4.1.1), yaitu, E = ˆe + E + + ˆe − E− + ˆz Ez, di mana E ± = (Ex + jEy) / 2,
menunjukkan bahwa Persamaan. (4.6.16) mengarah ke sistem homogen:
di mana ꞓ ± = ꞓ1 ± ꞓ2. Atau, tunjukkan bahwa dalam
basis polarisasi linear:
Untuk salah satu basis, pengaturan determinan matriks
koefisien ke nol, menunjukkan bahwa solusi E non nol ada asalkan N2 adalah
salah satu dari dua solusi:
Tunjukkan bahwa dua solusi untuk N2 adalah:
Anggota Kelompok 3
| Annisa Puspita Rahma Hafidz NIM : 1731130037 |
 |
| Ignatia Denada P. D. NIM : 1731130117 |
 |
| Muhammad Yusuf Habibie NIM : 1731130057 |