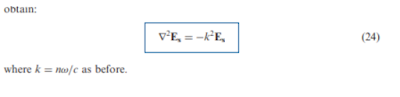Waveguide Dan Antenna Fundamentals
14.1 OPERASI DASAR WAVEGUIDE
Panduan gelombang mengasumsikan banyak bentuk berbeda yang bergantung pada tujuan panduan, dan pada frekuensi gelombang yang akan ditransmisikan. Bentuk paling sederhana (dalam hal analisis) adalah panduan pelat sejajar yang ditunjukkan pada Gambar 14.1. Bentuk lain adalah panduan pipa-berongga, termasuk panduan gelombang persegi panjang Gambar. 14.2, dan panduan silindris, ditunjukkan pada Gambar. 14.3. Panduan gelombang dielektrik, digunakan terutama pada frekuensi optik, termasuk panduan gelombang slab dari Gambar. 14.4 dan serat optik, ditunjukkan pada Gambar. 14.5. Masing-masing struktur ini memiliki keunggulan tertentu di atas yang lain, tergantung pada aplikasi dan frekuensi gelombang yang akan ditransmisikan.
Untuk mengembangkan pemahaman tentang perilaku panduan gelombang, kami mempertimbangkan panduan gelombang pelat paralel pada Gambar.14.1. Pada awalnya, kami mengenali ini sebagai salah satu struktur saluran transmisi yang kami selidiki di Bab. 13. Jadi pertanyaan pertama yang muncul adalah: Bagaimana panduan gelombang berbeda dari jalur transmisi untuk memulai? Perbedaannya terletak pada bentuk medan listrik dan magnet ketika saluran beroperasi sebagai saluran transmisi. Gelombang tegangan sinusoidal, dengan tegangan yang diterapkan antar konduktor, mengarah ke medan listrik yang diarahkan secara vertikal di antara konduktor seperti yang ditunjukkan. Karena arus mengalir hanya pada arah z, medan magnet akan berorientasi keluar masuk halaman (dalam arah y). Bidang interior terdiri dari gelombang elektromagnetik (TEM). Vektor gelombang k, ditunjukkan dalam gambar, menunjukkan arah perjalanan gelombang, serta arah aliran daya. Dengan sempurna melakukan lempeng, medan listrik antara pelat ditemukan dengan memecahkan Persamaan. (29), Bab. 11, mengarah ke Persamaan. (31) di bab itu.
Ketika frekuensi meningkat, perubahan yang luar biasa terjadi dalam cara bidang progagata di bawah garis. Meskipun konfigurasi lapangan asli Gambar. 14.6a mungkin masih ada, kemungkinan lain yang ditunjukkan pada Gambar
GAMBAR 14.1 Pemandu gelombang pelat paralel, dengan pelat logam pada x = 0, d. Di antara lempeng adalah dielektrik dari permitivitas €.
GAMBAR 14.2 Panduan gelombang persegi panjang
GAMBAR 14.3 Waveguide silindris.
GAMBAR 14.4 Diagram slab dielektrik simetris, dengan daerah lempeng (indeks bias n1) dikelilingi oleh dua dielektrik dari indeks n2
GAMBAR 14.5 Panduan gelombang serat optik, dengan dielektrik inti (r
GAMBAR 14.6 (A)
Listrik dan medan magnet dari modus TEM (saluran transmisi) di pandu pelat sejajar, membentuk gelombang pesawat yang merambat turun thr panduan sumbu. (B) gelombang Pesawat yang mencerminkan dari dinding budidaya dapat menghasilkan modus Waveguide yang tidak TEM lagi
Saluran transmisi terdiri dari dua atau lebih konduktor dan sebagai aturan akan mendukung gelombang TEM (atau sesuatu yang dapat mendekati gelombang tersebut). Seorang penulis waveguide dari satu atau lebih konduktor, atau tidak ada konduktor sama sekali, dan akan mendukung mode waveguide, bentuk yang mirip dengan yang dijelaskan di atas. Waveguides mungkin atau mungkin tidak mendukung gelombang TEM, tergantung pada desain.
Gelombang berkembang ke atas akan memiliki fase depan konkrit. Kondisi yang sama secara otomatis akan terjadi untuk semua gelombang yang merambat ke bawah. Ini adalah persyaratan untuk menetapkan mode panduan. sehingga persyaratan fase depan konkrit kita dipenuhi. Dari geometri kita melihat bahwa untuk setiap nilai m.

Panduan gelombang mengasumsikan banyak bentuk berbeda yang bergantung pada tujuan panduan, dan pada frekuensi gelombang yang akan ditransmisikan. Bentuk paling sederhana (dalam hal analisis) adalah panduan pelat sejajar yang ditunjukkan pada Gambar 14.1. Bentuk lain adalah panduan pipa-berongga, termasuk panduan gelombang persegi panjang Gambar. 14.2, dan panduan silindris, ditunjukkan pada Gambar. 14.3. Panduan gelombang dielektrik, digunakan terutama pada frekuensi optik, termasuk panduan gelombang slab dari Gambar. 14.4 dan serat optik, ditunjukkan pada Gambar. 14.5. Masing-masing struktur ini memiliki keunggulan tertentu di atas yang lain, tergantung pada aplikasi dan frekuensi gelombang yang akan ditransmisikan.
Untuk mengembangkan pemahaman tentang perilaku panduan gelombang, kami mempertimbangkan panduan gelombang pelat paralel pada Gambar.14.1. Pada awalnya, kami mengenali ini sebagai salah satu struktur saluran transmisi yang kami selidiki di Bab. 13. Jadi pertanyaan pertama yang muncul adalah: Bagaimana panduan gelombang berbeda dari jalur transmisi untuk memulai? Perbedaannya terletak pada bentuk medan listrik dan magnet ketika saluran beroperasi sebagai saluran transmisi. Gelombang tegangan sinusoidal, dengan tegangan yang diterapkan antar konduktor, mengarah ke medan listrik yang diarahkan secara vertikal di antara konduktor seperti yang ditunjukkan. Karena arus mengalir hanya pada arah z, medan magnet akan berorientasi keluar masuk halaman (dalam arah y). Bidang interior terdiri dari gelombang elektromagnetik (TEM). Vektor gelombang k, ditunjukkan dalam gambar, menunjukkan arah perjalanan gelombang, serta arah aliran daya. Dengan sempurna melakukan lempeng, medan listrik antara pelat ditemukan dengan memecahkan Persamaan. (29), Bab. 11, mengarah ke Persamaan. (31) di bab itu.
Ketika frekuensi meningkat, perubahan yang luar biasa terjadi dalam cara bidang progagata di bawah garis. Meskipun konfigurasi lapangan asli Gambar. 14.6a mungkin masih ada, kemungkinan lain yang ditunjukkan pada Gambar
GAMBAR 14.1 Pemandu gelombang pelat paralel, dengan pelat logam pada x = 0, d. Di antara lempeng adalah dielektrik dari permitivitas €.
GAMBAR 14.2 Panduan gelombang persegi panjang
GAMBAR 14.3 Waveguide silindris.
GAMBAR 14.4 Diagram slab dielektrik simetris, dengan daerah lempeng (indeks bias n1) dikelilingi oleh dua dielektrik dari indeks n2
GAMBAR 14.5 Panduan gelombang serat optik, dengan dielektrik inti (r

GAMBAR 14.6 (A)
Listrik dan medan magnet dari modus TEM (saluran transmisi) di pandu pelat sejajar, membentuk gelombang pesawat yang merambat turun thr panduan sumbu. (B) gelombang Pesawat yang mencerminkan dari dinding budidaya dapat menghasilkan modus Waveguide yang tidak TEM lagi
Saluran transmisi terdiri dari dua atau lebih konduktor dan sebagai aturan akan mendukung gelombang TEM (atau sesuatu yang dapat mendekati gelombang tersebut). Seorang penulis waveguide dari satu atau lebih konduktor, atau tidak ada konduktor sama sekali, dan akan mendukung mode waveguide, bentuk yang mirip dengan yang dijelaskan di atas. Waveguides mungkin atau mungkin tidak mendukung gelombang TEM, tergantung pada desain.
14.2 ANALISIS GELOMBANG GELOMBANG WAVEGUIDE PLAT
PARALLEL
Mari kita selidiki kondisi di mana
mode waveguide akan terjadi, menggunakan model gelombang bidang untuk bidang
mode. Pada Gambar 14.8a, jalur zig-zag ditampilkan lagi, tetapi fasa depan fase
ini diambil yang terkait dengan dua gelombang yang menyebar ke atas. Gelombang
pertama telah dipantulkan dua kali (di permukaan atas dan bawah) untuk
membentuk gelombang kedua (front fase yang merambat ke bawah tidak ditunjukkan).
Setelah puas
dengan kondisi ini untuk dua gelombang, kita akan menemukan semuanya..
GAMBAR 14.8
(A)
propagasi gelombang pesawat dalam panduan pelat paralel di mana sudut gelombang
sedemikian rupa sehingga gelombang propagasi ke atas tidak dalam fase. (B)
Sudut gelombang telah disesuaikan sehingga gelombang ke atas dalam fase,
sehingga dalam mode dipandu
Penggunaan
simbol βm untuk komponen z ku dan kd tepat karena m pada akhirnya akan menjadi
konstanta fasa untuk mode pandu gelombang ke dua, mengukur pergeseran fasa per
jarak ke bawah panduan; ini juga digunakan untuk menentukan fase velocit yof mode,
ω / βm, dan kecepatan kelompok, dω / dβm.
Sepanjang diskusi kita, kita akan
berasumsi bahwa medium di dalam panduan itu tanpa kehilangan dan bukan
magnetik, sehingga
yang kami
ungkapkan baik dalam hal konstanta dielektrik, € 'R, atau indeks bias, n, dari
medium.
Ini adalah Km, komponen x dari ku
dan kd, yang akan berguna bagi kita dalam mengukur kebutuhan kita pada fase
fase coincident melalui suatu kondisi yang dikenal sebagai resonansi
transversal. Kondisi ini menyatakan bahwa pergeseran fasa bersih yang diukur
selama perjalanan bolak-balik dimensi dimensi transversal penuh dari pemandu
harus merupakan kelipatan bilangan bulat dari 2π radian.
Pergeseran fase
total selama round-trip diperlukan untuk menjadi kelipatan bilangan bulat dari
2π:
Kmd+Ø+ Kmd+
Ø = 2m
Di mana 0 adalah pergeseran fase pada refleksi
di setiap batas. Perhatikan bahwa dengan 0 = (gelombang FE) atau 0 (gelombang FM) pergeseran fase
reflektif bersih selama round-trip adalah 2 π

GAMBAR
14.11
Pergeseran
fase gelombang pada refleksi dari permukaan konduksi sempurna tergantung pada
apakah gelombang insiden adalah TE (s-terpolarisasi) atau TM (p.
Terpolarisasi). di kedua gambar, medan listrik ditunjukkan karena mereka akan
muncul berbatasan langsung dengan batas konduksi. Dalam (a) bidang gelombang TE
membalikkan arah pada refleksi untuk membentuk bidang bersih nol pada batas.
Ini merupakan pergeseran fase x, sebagaimana terbukti dengan mempertimbangkan
gelombang transmisi fiktif (hukum putus-putus), yang dibentuk oleh rotasi
sederhana dari gelombang yang dipantulkan menjadi sejajar dengan gelombang
datang. Dalam (b) gelombang TM insiden mengalami pembalikan komponen z medan
listriknya. Bidang resultan dari gelombang yang dipantulkan, bagaimanapun,
sebelum fase-bergeser; memutar gelombang yang dipantulkan menjadi sejajar
dengan gelombang insiden (garis putus-putus).
atau 0, terlepas
dari sudut insidensinya. Dengan demikian pergeseran fase reflektif tidak ada
kaitannya dengan masalah saat ini, dan kita dapat menyederhanakan (3) untuk
membaca:
yang
berlaku untuk mode TE dan TM. Catatan dari Gambar 14.9 bahwa Km =
k cos Øm. Dengan demikian sudut gelombang untuk mode yang
diizinkan dapat ditemukan dari (4) dengan (2):
Dimana
λ adalah panjang gelombang dalam ruang bebas. Selanjutnya kita dapat memecahkan
konstanta fase untuk setiap mode, menggunakan (1) dengan (4):
Signifikansi
frekuensi cutoff mudah dilihat dari (8): Jika frekuensi operasi, ω, lebih besar
daripada frekuensi cutoff untuk mode m,
maka mode tersebut akan memiliki fase βm konstan, yang bernilai
nyata, dan begitu mode akan menyebar w <
 , adalah imajiner, dan mode
tidak menyebar.
, adalah imajiner, dan mode
tidak menyebar.

Terkait
dengan frekuensi cutoff adalah panjang gelombang cutoff , didefinisikan sebagai
panjang gelombang ruang bebas di mana cutoff untuk mode m terjadi. Ini akan
menjadi
, didefinisikan sebagai
panjang gelombang ruang bebas di mana cutoff untuk mode m terjadi. Ini akan
menjadi
 , didefinisikan sebagai
panjang gelombang ruang bebas di mana cutoff untuk mode m terjadi. Ini akan
menjadi
, didefinisikan sebagai
panjang gelombang ruang bebas di mana cutoff untuk mode m terjadi. Ini akan
menjadi
Perhatikan,
misalnya, bahwa dalam panduan yang diisi udara (n = 1) panjang gelombang di
mana mode orde terendah pertama mulai menyebar adalah  = 2d, atau pemisahan pelat
adalah setengah panjang gelombang. Mode m akan menyebar kapan saja λ> λ_cm
atau ekivalen setiap kali
= 2d, atau pemisahan pelat
adalah setengah panjang gelombang. Mode m akan menyebar kapan saja λ> λ_cm
atau ekivalen setiap kali  <
<  . Penggunaan panjang
gelombang cutoff memungkinkan kita untuk membangun bentuk Eq yang berguna
kedua. (8):
. Penggunaan panjang
gelombang cutoff memungkinkan kita untuk membangun bentuk Eq yang berguna
kedua. (8):
 = 2d, atau pemisahan pelat
adalah setengah panjang gelombang. Mode m akan menyebar kapan saja λ> λ_cm
atau ekivalen setiap kali
= 2d, atau pemisahan pelat
adalah setengah panjang gelombang. Mode m akan menyebar kapan saja λ> λ_cm
atau ekivalen setiap kali  . Penggunaan panjang
gelombang cutoff memungkinkan kita untuk membangun bentuk Eq yang berguna
kedua. (8):
. Penggunaan panjang
gelombang cutoff memungkinkan kita untuk membangun bentuk Eq yang berguna
kedua. (8):
14.3 PARALEL-PLATE GUIDE
ANALISIS MENGGUNAKAN GELOMBANG PERSAMAAN
Itu paling langsung pendekatan di itu analisis dari
setiap pandu adalah melalui gelombang persamaan, yang kita memecahkan subyek untuk itu batas
kondisi di dinding melakukan. Itu bentuk dari itu persamaan bahwa kita akan menggunakan aku s bahwa
dari Eq. (12) di Detik. 11.1, yang ditulis untuk itu kasus dari ruang bebas perambatan. Kita account
untuk sifat dielektrik di Waveguide oleh menggantikan 1/0 di bahwa persamaan dengan k untuk
Kita dapat menggunakan itu hasil
dari terakhir bagianuntuk membantu memvisualisasikan proses pemecahan persamaan
gelombang. Untuk
Sebagai contoh, kita dapat mempertimbangkan mode TE pertama, di mana akan ada hanya komponen ay E. The
persamaan gelombang menjadi:
Kami berasumsi bahwa itu lebar dari Petunjuk (Di mereka arah) sangat besar dibandingkan pemisahan piring, d.
Oleh karena itu kita dapat mengasumsikan tidak ada y variasi di Lapangan (fringing
bidang yang diabaikan), dan sebagainya 02Erhari2
= 0. Kita juga tahu bahwa itu z variasi akan menjadi formulir TOPI'. Itu bentuk dari itu
bidang solusi akan dengan demikian
dimana Eo adalah Sebuah konstan, dan dimana f “, (x) aku s Sebuah fungsi normal menjadi menghalangiberanjau (yang maksimum nilai adalah
kesatuan). Kita
memiliki
termasuk tanda tangan m di P, K, dan f(X), sejak kita mengharapkan
beberapa solusi
bahwa sesuai untuk
mode diskrit, untuk
yang kita modus kaitkan jumlah, m. Kita
sekarang pengganti (26) ke (25) untuk mendapatkan:
Catatan juga bahwa kami telah menulis (27) menggunakan jumlah seluruhnya turunan, d2/ E & sejak f “, aku s Sebuah fungsi hanya dari x. Kita make berikutnya menggunakan dari itu geometri
Gambar. 14,9, dan catatan bahwa k2 - R ,, = menggunakan ini di (27) kita mendapatkan
Umum larutan (28) akan menjadi
0,41
(x) = cos (x ,,, r) sin (x ,,, x) (29)
Kita berikutnya menerapkan itu
batas yang sesuai kondisi
di kami masalah untuk evaluasi Km. Dari Gambar. 14,1, melakukan batas-batas muncul di x
= 0 dan x = d, di mana medan listrik tangensial (Ex) harus menjadi nol. Di Eq. (29), hanya dosa (x “pc) jangka akan mengizinkan kondisi batas untuk menjadi puas, sehingga kami mempertahankan itu dan
menghentikan istilah cosinus. x =
0 kondisi aku s otomatis puas dengan itu sinus fungsi. Itu x = d kondisi bertemu kapan kami
memilih nilai dari km seperti dibawah ini
Kita mengakui Eq. (30)
sebagai itu sama hasil bahwa kita diperoleh dengan menggunakan itu melintang resonansi
kondisi dari itu terakhir bagian. Akhir bentuk dari en, aku s diperoleh oleh penggantinya fm (Y) sebagai diungkapkan
melalui (29) dan (30) ke (26), menghasilkan
hasilnya bahwa aku s konsisten dengan yang satu menyatakan
dalam Pers. (14):
. Itu gelombang harus resonan
dalam struktur, yang berarti bahwa net perjalanan pulang pergi tahap shift 2 juta.
Dengan gelombang pesawat berorientasi vertikal, sirip, = 0, dan
begitu di memotong
berpaling di itu x arah jika itu panjang gelombang yang diukur di medium aku s sebuah bilangan bulat kelipatan dari 2d,
dimana itu bilangan bulat aku s tn.
Setelah
menemukan medan listrik, kita dapat menemukan medan magnet menggunakan
persamaan Maxwell. Kami mencatat dari model gelombang pesawat kami yang kami
harapkan untuk mendapatkan x dan e komponen H,untuk modus TE. Kami
menggunakan persamaan Maxwell
Kami
memecahkan
H, oleh membagi kedua sisi
(35) oleh
-fon /. Pertunjukan ini operation
pada (36), kita memperoleh
itu dua magnetik komponen medan:
Bersama-sama, dua komponen ini membentuk pola loop tertutup untuk H, di x, pesawat, seperti
yang dapat diverifikasi menggunakan itu mempersingkat merencanakan metode yang dikembangkan di Detik. 2.6,
di mana 9 =, Ct /
E.
hasil ini
konsisten dengan
kami pemahaman
tentang mode Waveguide berdasarkan itu superposisi dari
gelombang pesawat, di yang itu hubungan antara E, dan H, aku s melalui medium hakiki impedansi, rp.
Kelompok 7
Kelompok 7
 |
| ARLAMSAN AJI PRASETYO / 1731130103 |
 |
| Ramadhaniar Sekarsari / 1731130018 |
 |
| Daniyal Mahendra / 1731130115 |