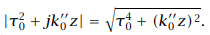Propagasi Pulsa dalam Media Dispersif
Karena F (ˆ 0, ω - ω0) membatasi jangkauan integrasi efektif dalam Persamaan. (3.5.5) untuk sebuah band yang sempit tentang ω0, satu dapat memperluas k (ω) untuk seri Taylor tentang ω0 dan tetap hanya beberapa hal pertama:
3. Propagasi Pulsa dalam Media Dispersif
Gambar. 3.5.2 Amplop pulpa menjalar dengan kecepatan
vg tetap tidak berubah bentuknya.
Integral ini dapat dilakukan dengan tepat, dan
mengarah ke ekspresi berikut dalam kasus aproksimasi linier dan kuadrat (dengan
asumsi bahwa k_0^', k_0^''adalah nyata):
Respons frekuensi yang sesuai mengikuti dari Persamaan.
(3.5.15), menggantikan ω 'oleh ω:
Kasus linear diperoleh dari yang kuadrat dalam batas
k_0^'' → 0. Kami mencatat bahwa integral dari Persamaan. (3.5.15), serta contoh
pulsa gaussian yang kita pertimbangkan nanti, adalah kasus khusus integral
Fourier berikut: di
dimana a, b adalah nyata, dengan pembatasan
bahwa ≥ 〖0.〗^† Integral untuk g (z, t ) sesuai dengan
kasus a = 0 dan b = k_0^''z. Menggunakan (3.5.16) ke (3.5.8), kita memperoleh
Persamaan. (3.5.13) dalam kasus linear dan ekspresi convolutional berikut dalam
kuadrat satu:
dan dalam domain frekuensi:
3,6 Grup Velocity Dispersion dan Pulse Menyebarkan
Dalam pendekatan linear, amplop merambat dengan
kelompok kecepatan V_gtersisa tidak berubah di bentuk. Tetapi dalam pendekatan
kuadrat, sebagai konsekuensi dari Persamaan. (3.5.19), ia menyebar dan
mengurangi amplitudo dengan jarak z, dan itu berkicau. Untuk melihat ini,
mempertimbangkan pulsa masukan gaussian lebar efektif τ_0:
dengan
transformasi Fourier  ( 0, ω) dan
( 0, ω) dan  ( 0, ω)=
( 0, ω)=  ( 0, ω − ω0):
( 0, ω − ω0):
dengan lebar efektif Δω = 1/τ_0Dengan demikian,
kondisi Δω « ω_0, mensyaratkan bahwa τ_0ω0» 1, yaitu, sebuah amplop dengan
durasi panjang relatif terhadap periode operator. Amplop yang disebarkan F (z,
t) dapat ditentukan dari Persamaan. (3.5.19) atau dari (3.5.20). Dengan
menggunakan yang terakhir, kita memiliki:
Integral Fourier (3.5.18), kemudian, memberikan amplop yang
disebarkan dalam domain waktu:
Jadi, secara efektif kita memiliki penggantian τ_0^2→ τ_0^2+jk_0^'' z. Dengan asumsi untuk
momen yang k_0^' dan k_0^(' ') adalah nyata, kita menemukan untuk besarnya
pulsa yang disebarkan:
dimana kita menggunakan
properti Lebar efektif ditentukan dari argumen
eksponen:
Oleh karena itu, lebar pulsa
meningkat dengan jarak z. Juga, amplitudo pulsa menurun dengan jarak, yang
diukur misalnya pada puncak maksimum: Maksimum
puncak terjadi pada tundaan grup t = k_0^'z, dan
karenanya ia bergerak pada kecepatan kelompok vg = 1/k_0^'. Pengaruh penyebaran
pulsa dan pengurangan amplitudo karena istilah k_0^''disebut sebagai dispersi
kecepatan kelompok atau dispersi kromatik. Gambar 3.6.1 menunjukkan amplitudo.
3. Propagasi Pulsa dalam Media Dispersif

menurunkan dan menyebarkan pulsasi dengan jarak,
serta efek kicau (akan
dibahas di bagian berikutnya.)
Karena lebar frekuensi Δω = 1 / τ0, kita dapat
menulis selisih waktu berlebih Δτ = k_0^''z / τ0 dalam bentuk Δτ = k_0^''zΔω.
Ini dapat dipahami dalam hal perubahan dalam penundaan grup. Ini mengikuti dari
t_g = z/V_g = k’z
bahwa perubahan t_g karena Δω akan:
Dalam transmisi data digital menggunakan serat
optik, masalah pelebaran pulsa yang diukur oleh (3.6.8) menjadi penting karena
membatasi laju bit maksimum yang dapat digunakan, atau secara ekuivalen , jarak
propagasi maksimum. Interval waktu interpulse, katakanlah, T_b detik dengan mana pulsa bit dipisahkan sesuai
dengan laju data f_b = 1/T_bbit / detik
dan harus lebih lama dari waktu yang meluas, T_b > ΔV_g, sebaliknya pulsa yang melebar akan
mulai tumpang tindih mencegah identifikasi yang jelas sebagai terpisah.
3.6. Group Velocity Dispersion dan
Pulse Spreading
Ini membatasi jarak propagasi z ke nilai maksimum:
Karena D = Δt_gzΔλ, parameter D biasanya diukur
dalam satuan picosecond per km per nanometer-km yang mengacu pada jarak z dan
nm ke panjang gelombang menyebar Δλ. Demikian pula, parameter k’’ = Δt_g/zΔω
diukur dalam satuan ps² / km. Sebagai contoh, kami menggunakan model Sellmeier
untuk leburan silika yang diberikan dalam Persamaan. (1.11.16) untuk plot pada
Gambar. 3.6.2 indeks bias n (λ) dan koefisien dispersi D (λ) terhadap panjang
gelombang dalam kisaran 1 ≤ λ ≤ 1.6 μm.
Kami mengamati bahwa D lenyap, dan karenanya juga k
'' = 0, pada sekitar λ = 1,27 μm sesuai dengan penyebaran dispersi. Panjang
gelombang ini disebut sebagai "nol panjang gelombang dispersi."
Namun, panjang gelombang operasi yang disukai adalah λ = 1,55 μm di mana
kerugian serat diminimalkan. Pada λ = 1,55, kami menghitung nilai indeks bias
berikut dari persamaan Sellmeier:
3. Propagasi Pulsa dalam Media Dispersif
dengan
koefisien dispersi D (λ) diberikan kira-kira oleh bentuk linearisasi yang
dipasang di sekitar 1,55 μm:
Selain
itu, serat standar memiliki panjang gelombang dispersi nol sekitar 1,31 μm dan
konstanta pelemahan sekitar 0,2 dB / km.
3.7. Propagasi dan Kicau
Lebar efektif puncak
menggeneralisasi Persamaan. (3.6.6)
Dari bagian imajiner Persamaan. (3.6.17), kami
mengamati dua efek tambahan. Pertama, koefisien non-nol dari istilah jt setara
dengan pergeseran frekuensi dependen-z dari frekuensi pembawa ω0, dan kedua,
dari koefisien jt² / 2, akan ada sejumlah kicauan seperti yang didiskusikan di
bagian berikutnya. bagian. Pergeseran frekuensi dan koefisien kicauan
(generalisasi Persamaan (3.7.6)) berubah menjadi:
3.7 Propagasi dan Kicau
Sebuah
sinusoid cicit memiliki frekuensi sesaat yang berubah secara linear dengan
waktu, disebut sebagai modulasi frekuensi linier (FM). Hal ini diperoleh dengan
substitusi: di
3. Propagasi Pulsa dalam Media Dispersif
Dengan demikian, lebar yang kompleks dihargai dikaitkan
dengan kicauan linier. Sebuah pulsa gaussian yang tidak disirkulasikan yang
menyebar dengan jarak z ke media menjadi berkicau karena memperoleh lebar yang
kompleks, yaitu, τ_0^2+ jk_0^'' z,
seperti yang diberikan oleh Persamaan. (3.6.4)
3. Propagasi Pulsa dalam Media
Dispersif
dan dalam domain waktu:
Ada
banyak cara untuk menerapkan filter kompensasi dispersi dalam aplikasi serat
optik
Metode
terakhir adalah salah satu yang paling banyak digunakan dan digambarkan di
bawah ini
3,9. Lambat, Cepat, dan Negatif Grup
Kecepatan yang
Beroperasi
pada resonansi adalah bukan ide yang baik karena jumlah yang cukup
besarpelemahan atau keuntungan yang
timbul dari bagian imajiner dari indeks bias, yang
akan menyebabkan distorsi amplitudo
dalam sinyal seperti itu merambat.
Memilih
puncak yang lebih dekat terpisah di baris ketiga grafik, memiliki efek
meningkatkan kemiringan negatif dari nr, sehingga menyebabkan indeks kelompok
menjadi negatif pada titik tengah, Re (ng) <0, menghasilkan kecepatan
kelompok negatif, vg <0.
Ekspresi
berikut digunakan pada Gambar 3.9.2 untuk indeks bias dan kelompok, dengan f =
1 untuk kasus penyerapan, dan f = −1 untuk kasus penguatan:
Kedua
puncak ditempatkan secara simetris tentang frekuensi titik tengah ω0, yaitu
pada ω1 = ω0 - Δ dan ω2 = ω0 + Δ, dan garis linewidth γ dipilih. Nilai-nilai
numerik tertentu yang digunakan dalam grafik ini adalah:
(atas, lambat) f = +1 , ωp = 1 , ω0 = 5 , Δ
= 0.25 , γ = 0.1
(tengah, cepat) f = −1 , ωp = 1 , ω0 = 5 , Δ
= 0.75 , γ = 0.3
(bawah, negatif) f = −1 , ωp = 1 , ω0 = 5 ,
Δ = 0.50 , γ = 0.2
3.10. Kicauan Radar dan Kompresi Pulsa (113)
telah memasuki medium penyerap dan dilemahkan ketika merambat saat tertinggal di belakang pulsa vakum yang setara karena vg <c.
Pada t = 120, sementara puncaknya masih dalam medium penyerap, ekor depan telah melewati daerah vakum tengah dan telah masuk ke dalam medium gain di mana ia mulai mendapatkan penguat. Pada t = 180, puncak telah pindah ke daerah vakum tengah, tetapi ekor depan telah cukup diperkuat oleh media gain dan mulai membentuk puncak yang ekornya sudah keluar ke dalam wilayah vakum paling kanan.
3. Propagasi Pulsa dalam Media Dispersif (114)
SNR di penerima diberikan oleh:
SNR = (E rec)/N0 = (P rec T)/N0
di mana Prec dan Erec = PrecT menunjukkan kekuatan dan energi dari pulsa yang diterima, dan N0 adalah kepadatan spektrum daya noise yang diberikan dalam hal suhu gangguan efektif Te penerima oleh N0 = kTe. bahwa daya yang diterima Prec sebanding dengan daya pemancar Ptr dan berbanding terbalik dengan kekuatan keempat dari jarak R. Dengan demikian, untuk menjaga SNR pada tingkat terdeteksi untuk jarak besar, daya pemancar yang besar dan energi pulsa yang sesuai Etr = PtrT harus bekas.
3. Propagasi Pulsa dalam Media Dispersif (114)
SNR di penerima diberikan oleh:
SNR = (E rec)/N0 = (P rec T)/N0
di mana Prec dan Erec = PrecT menunjukkan kekuatan dan energi dari pulsa yang diterima, dan N0 adalah kepadatan spektrum daya noise yang diberikan dalam hal suhu gangguan efektif Te penerima oleh N0 = kTe. bahwa daya yang diterima Prec sebanding dengan daya pemancar Ptr dan berbanding terbalik dengan kekuatan keempat dari jarak R. Dengan demikian, untuk menjaga SNR pada tingkat terdeteksi untuk jarak besar, daya pemancar yang besar dan energi pulsa yang sesuai Etr = PtrT harus bekas.
3. Propagasi Pulsa dalam Media Dispersif (114)
SNR di penerima diberikan oleh:
SNR = (E rec)/N0 = (P rec T)/N0
di mana Prec dan Erec = PrecT menunjukkan kekuatan dan energi dari pulsa yang diterima, dan N0 adalah kepadatan spektrum daya noise yang diberikan dalam hal suhu gangguan efektif Te penerima oleh N0 = kTe. bahwa daya yang diterima Prec sebanding dengan daya pemancar Ptr dan berbanding terbalik dengan kekuatan keempat dari jarak R. Dengan demikian, untuk menjaga SNR pada tingkat terdeteksi untuk jarak besar, daya pemancar yang besar dan energi pulsa yang sesuai Etr = PtrT harus bekas.
3. kicauan radar dan kompresi pulsa 121
Memperhatikan bahwa (ωd + ω˙0t) T = 2π (fdT + Bt), dan mengganti t oleh t − td untuk mengembalikan penundaan kedatangan pulsa yang diterima, kita memperoleh:
E compr(t,fd) = √jBT e^(jw0(t-td)-jw0(t-td)/2) Sin[ח(fdT + B(t - td))] / ח(fdT + B(t – td))
Terlihat bahwa puncak pulsa tidak lagi terjadi pada t = td, tetapi lebih pada waktu yang bergeser fdT + B (t −td) = 0, atau, t = td −fdT / B, menghasilkan ambiguitas potensial. dalam jangkauan. Kami menemukan:
3. Propagasi Pulsa dalam Media Dispersif (124)
2.12. Masalah
yang dapat ditulis dalam bentuk normalisasi:
E(ω) = √(2חf/ω0) e^(-j(w-w0)/2w0) , D(ω) = (F(W+)-F(W-))/(1-j)
di mana w ± didefinisikan oleh:
w± = √(ω0/ח) (±T/2 – ω - ω0/ω0) = √2BT (±1/2 – f-f0/B)
2.12. Masalah
yang dapat ditulis dalam bentuk normalisasi:
E(ω) = √(2חf/ω0) e^(-j(w-w0)/2w0) , D(ω) = (F(W+)-F(W-))/(1-j)
di mana w ± didefinisikan oleh:
w± = √(ω0/ח) (±T/2 – ω - ω0/ω0) = √2BT (±1/2 – f-f0/B)
Faktor ini memiliki besaran yang secara efektif terbatas dalam band ideal | f - f0 | ≤ B / 2 dan fase yang tetap hampir nol dalam band yang sama, dengan kedua properti ini meningkat dengan meningkatnya produk bandwidth-waktu BT. † Jadi, pilihan untuk filter kompresi yang dibuat berdasarkan fase fase kuadrat dibenarkan.