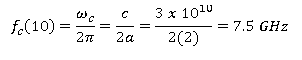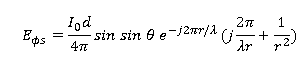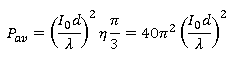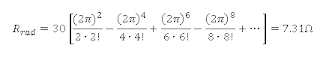14.4 - 14.6
14.4 GELOMBANG
REKANGULER
Pada bagian ini kami
mempertimbangkan gelombang persegi
panjang, struktur yang banyak digunakan yang biasanya digunakan dalam wilayah
gelombang mikro spektrum elektromagnetik. Analisis singkat tentang struktur
akan dipaparkan di sini, dengan tujuan untuk mempertahankan fitur operasional
utama dan tes khusus dari panduan ini. Pembaca disebut Ref. 1 untuk studi lebih
lanjut.
Panduan persegi ditunjukkan pada
Gambar 14.2. Kita dapat menghubungkan struktur ini dengan yang ada pada panduan
pelat paralel dari bagian sebelumnya dengan memikirkannya sebagai dua pemandu
arah paralel dari orientasi ortogonal yang dirakit untuk membentuk satu unit.
Dengan demikian kita memiliki sepasang dinding konduksi horisontal (sepanjang arah
x) dan sepasang dinding vertikal (sepanjang y), yang semuanya sekarang
membentuk satu batas yang berkelanjutan. Persamaan gelombang dalam bentuk tiga
dimensi penuh (Persamaan. (25)) sekarang harus dipecahkan, karena secara umum
kita mungkin memiliki variasi bidang di ketiga arah koordinat. Dengan asumsi
bahwa variasi dengan z akan menjadi hanya seperti sebelumnya,
Persamaan
ini membawa 10 pikiran masalah persamaan Laplace dua dimensi dari Sec. 7.5, di
mana metode solusi product digunakan. Metode dasar yang sama digunakan 10
memecahkan (42) juga, dan solusi resulling mengambil bentuk umum
di mana 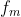 dan
dan 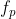 adalah sinus atau cosinus. Dua bilangan bulat,
m dan p, sekarang diperlukan untuk menggambarkan berbagai bidang dalam
arah x dan y. Sekali lagi, kami prihatin dengan mode TE dan TM, dan persamaan
gelombang diselesaikan secara terpisah untuk masing-masing jenis.
adalah sinus atau cosinus. Dua bilangan bulat,
m dan p, sekarang diperlukan untuk menggambarkan berbagai bidang dalam
arah x dan y. Sekali lagi, kami prihatin dengan mode TE dan TM, dan persamaan
gelombang diselesaikan secara terpisah untuk masing-masing jenis.
Dari
sini, masalahnya menjadi rumit dan melampaui ruang lingkup (dan tujuan) dari
pengobatan t sekarang. Sebaliknya, banyak yang dapat dipelajari tentang panduan
ini melalui intuisi kita, dan melalui pengetahuan kita tentang panduan
paralel-pla te. Ternyata mode yang paling penting dalam waveguide persegi
panjang adalah bentuk yang sama dengan struktur pelat paralel. Pertimbangkan,
misalnya, kemunculan mode TE dalam panduan recta ngular. Medan listrik dari
mode seperti itu dapat muncul seperti ditunjukkan pada Gambar. 14.13a, di mana
lapangan secara vertikal pola dirata, dan termina tes pada pelat atas dan
bawah. Medan juga menjadi nol pada dua dinding vertikal, seperti yang diperlukan
dari kondisi batas kami pada medan listrik tangen di permukaan kondensasi. Mari
kita mempertimbangkan kasus di mana lapangan tidak menunjukkan variasi dengan
y, tetapi bervariasi dengan x dan z (yang terakhir menurut ). Karena itu,dalam persamaan gelombang
(42) menurun dan persamaannya menjadi identik dalam bentuk ke (27), yang
digunakan untuk panduan paralel-pla te. Solusi bidang demikian identik dalam
bentuk untuk (31), (37) dan (38), tetapi dengan beberapa perbedaan notasi kecil:
GAMBAR 14.13
Mode konfigurasi medan
listrik dalam pandu gelombang persegi.
dimana
Contoh 14.4
Sebuah pandu gelombang persegi yang berisi udara memiliki
dimensi a = 2 cm dan b = 1 cm. Tentukan rentang frekuensi di mana panduan akan
mengoperasikan mode tunggal.
Solusi. Karena panduan ini berisi udara, n = I, dan (48)
memberi, untuk m = 1:.
Modus orde tinggi selanjutnya yang, dari (48) dan (54),
akan memiliki frekuensi cutoff yang sama, karena a = 2b. Frekuensi ini akan dua
kali t hat ditemukan untuk , atau 15 GHz. Dengan
demikian rentang frekuensi operasi di mana pemandu akan menjadi mode tunggal
adalah 7.5 GHz <f < 15 GHz.
Perbedaan mendasar yang penting antara pandu
gelombang persegi (atau panduan pipa berongga) dan saluran transmisi adalah
bahwa panduan persegi panjang tidak akan mendukung mode TEM. Kami telah
menunjukkan ini dalam penelitian kami tentang gelombang TE. Fakta bahwa panduan
ini dibentuk dari struktur logam yang sepenuhnya tertutup berarti bahwa medan
elektrik apapun yang disebut di bidang transversal harus menunjukkan variasi
dalam bidang; ini karena semua komponen medan listrik terpilih yang
bersinggungan dengan konduktor harus nol pada batas konduksi. Sejak E varies di
bidang transversal, penghitungan H melalui ∇ x E = H harus mengarah ke komponen z dari H, dan jadi
kita tidak bisa memiliki mode TEM. Kita tidak dapat menemukan orientasi lain
dari E yang benar-benar melintang dalam panduan yang akan memungkinkan H. yang
benar-benar melintang
Ketika efek kehilangan
kulit menjadi berlebihan, cara yang baik untuk menghapusnya adalah dengan
menghilangkan logam dalam struktur sepenuhnya, dan menggunakan antarmuka antara
dielektrik untuk permukaan confini. Kami dengan demikian memperoleh panduan
gelombang dielektrik; bentuk dasar, pandu gelombang slab simetris, ditunjukkan
pada Gambar 14.14. Struktur ini dinamakan demikian karena simetri vertikalnya
tentang sumbu z. Panduan diasumsikan memiliki lebar dalam y yang jauh lebih
besar daripada ketebalan pelat, d, sehingga masalah menjadi dua dimensi, dengan
bidang yang dianggap bervariasi dengan x dan z sementara tidak bergantung pada
y. Panduan slab bekerja dengan cara yang sangat mirip dengan waveguide pelat
paralel, kecuali refleksi gelombang terjadi pada antarmuka antara dielektrik,
memiliki indeks refraktif yang berbeda, n_1 untuk slab, dan n_1 untuk daerah surrou nding di atas dan di
bawah. Dalam panduan dielektrik, refleksi total diperlukan, sehingga sudut
insiden harus melebihi sudut kritis. Akibatnya, seperti yang dibahas dalam Sec.
12,5, indeks lempengan, n_1, harus lebih besar dari bahan sekitarnya, n_2.
Panduan dielektrik berbeda dari panduan konduksi konduktor dalam kekuatan yang
tidak terbatas pada pelat, tetapi berada di atas dan di bawah sebagian.
Panduan dielektrik digunakan secara prima rily pada
frekuensi optik (pada urutan 〖10〗^14
Hz). Sekali lagi, panduan dimensi melintang harus disimpan pada urutan panjang
gelombang untuk mencapai operasi dalam mode tunggal. Sejumlah metode fabrikasi
dapat digunakan untuk mencapai hal ini. Sebagai contoh, sebuah plate kaca dapat
didoping dengan bahan yang akan menaikkan indeks bias. Proses doping
memungkinkan n1aterials untuk diperkenalkan hanya dalam lapisan tipis yang
berdekatan dengan permukaan yang beberapa mikrometer tebal.
Untuk memahami bagaimana panduan beroperasi, perhatikan
Gambar 14.15, yang menunjukkan gelombang yang bergerak melalui lempengan dengan
memantulkan banyak ion, di mana transmisi parsial ke daerah atas dan bawah
terjadi pada setiap bouncing. Vektor Wa ditampilkan di daerah tengah dan atas,
bersama dengan komponennya di arah x dan z. Seperti yang kami temukan di Chap.
12, komponen z (β) dari semua wavevectors adalah sama, seperti harus benar jika
kondisi batas medan di dalam terfaces harus dipenuhi untuk semua ion dan waktu
posit. Pengambilan parsial di daerah perbatasan adalah, tentu saja, situasi
undesi rable, karena kekuasaan di pelat akhirnya akan bocor. Kami telah
memiliki propagasi gelombang bocor di dalam struktur
GAMBAR 14.14
Struktur pandu gelombang
dielektrik simetris, di mana gelombang merambat sepanjang z. Panduan
diasumsikan tidak terbatas ke arah mereka, sehingga membuat masalah menjadi dua
dimensi
GAMBAR 14.15
Geometri gelombang
pesawat dari gelombang bocor di waveguide .slab simetris. Untuk mode panduan,
refleksi total terjadi di interior, dan komponen x dari k_2u dan k_2d
adalah imajiner.
Sekarang,
dari geometri Gambar 14.15, kita dapat membangun distribusi medan gelombang TE
dalam panduan menggunakan superposisi gelombang pesawat. Di wilayah lempengan -d/2<x<d/2), kita punya
dimana
dan
Di daerah di atas dan
di bawah lempengan, gelombang merambat sesuai dengan gelombang vektor k_2u dan
k_2d seperti ditunjukkan pada Gambar
14.15. Misalnya, di atas pelat (x> d / 2), medan listrik TE akan berupa:
GAMBAR 14.16
Distribusi amplitudo medan listrik di atas bidang
transversal untuk tiga mode pertama dalam panduan slab simetris
Menerapkan kondisi di atas lO
(65), (66), (70), dan (71) menghasilkan kembali dalam ekspresi akhir untuk
medan listrik di pandu gelombang slmclric slab, untuk kasus-kasus genap ganjil
dan ganjil:
Contoh 14.5
Panduan
Lempeng dielektrik asimetris adalah untuk memandu cahaya pada panjang gelombang
I = 1,30 Am. Ketebalan lempengan adalah d = 5,00 Am, dan indeks bias bahan
sekitarnya adalah n2 = 1,450. Tentukan indeks bias maksimum yang diizinkan dari
bahan lempengan yang akan memungkinkan operasi mode TE dan TM tunggal.
Solusi.
Eq. (79) dapat ditulis dalam bentuk:
jadi
Jelas
sekali, toleransi fabrikasi sangat berat saat membangun panduan dielektrik
untuk operasi mode tunggal!
Panduan
gelombang serat optik bekerja pada prinsip yang sama dengan panduan dielektrik
dasar, kecuali, tentu saja untuk penampang bulat bulat. Sebuah serat indeks
langkah ditunjukkan pada Gambar. 14,5 di mana inti indeks tinggi jari-jari a
dikelilingi oleh indeks bawah yang lebih rendah dari jari-jari b. Cahaya
terbatas pada inti melalui mekanisme refleksi total, tetapi sekali lagi
beberapa fraksi daya berada di cladding juga. Seperti yang kami temukan di
panduan lempengan, kekuatan kelongsong kembali bergerak ke arah inti saat
frekuensi dinaikkan. Selain itu, sebagaimana benar dalam slab waveguide, serat
mendukung mode yang tidak memiliki cutoff. Sekali lagi, tanpa bukti (tetapi
lihat Pustaka 2 atau 3), kondisi untuk operasi mode tunggal dalam serat indeks
langkah ditemukan serupa dengan yang ada di pelat
Dimensi khas dari
serat mode tunggal termasuk diameter inti antara 5 dan 10 μm, dengan diameter
cladding biasanya 125 μm. Seperti yang kami temukan pada contoh di atas,
perbedaan indeks bias antara inti dan cladding sangat kecil, dan biasanya
merupakan pecahan kecil dari satu persen.
D14.7 Sebuah 0.5 mm lempeng kaca tebal (n_1=1.45)
dikelilingi oleh udara (n_2=1). Panduan lempengThe slabguides cahaya inframerah
pada panjang gelombang λ=1.0 μm. Berapa banyak mode TE dan ™ yang akan
menyebar?
Jawaban.
2101
14.6 Prinsip Prinsip Antena Dasar
Pada bagian akhir ini kami mengeksplorasi
beberapa konsep tentang radiasi energi elektromagnetik dari antena dipol sederhana.
Diskusi lengkap tentang antena dan aplikasinya membutuhkan beberapa bab atau
seluruh buku. Tujuan kami adalah untuk menghasilkan pemahaman mendasar tentang
bagaimana medan elektromagnetik memancar dari distribusi saat ini. Jadi untuk
pertama kalinya, kita akan memiliki bidang spesifik yang dihasilkan dari sumber
waktu tertentu. Dalam diskusi tentang gelombang dan medan dalam media massal
dan dalam waveguides, hanya gerakan gelombang dalam medium yang diselidiki, dan
sumber-sumber ladang tidak dipertimbangkan. Distribusi arus dalam konduktor
adalah masalah yang sama, meskipun kami setidaknya menghubungkan arus dengan
intensitas medan listrik yang diasumsikan pada permukaan konduktor. Ini mungkin
dianggap sebagai sumber, tetapi ini bukan yang sangat praktis karena itu tidak
terbatas luasnya.
Kami
sekarang mengasumsikan filamen saat ini (penampang sangat kecil) sebagai
sumber, diposisikan dalam media tanpa batas yang tak terbatas. Filamen diambil
sebagai panjang diferensial, tetapi kita akan dapat memperluas hasil dengan
mudah ke filamen yang pendek dibandingkan dengan panjang gelombang, khususnya
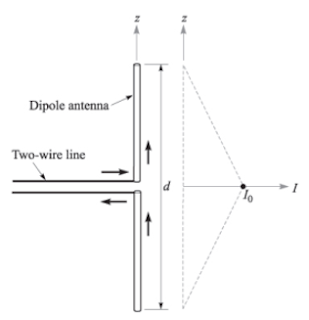
kurang dari sekitar seperempat panjang gelombang secara keseluruhan. Filamen diferensial
ditunjukkan pada titik asal dan diorientasikan sepanjang sumbu z pada Gambar
14.17. Rasa positif dari arus diambil dalam arah a_z. Kami mengasumsikan arus
seragam I_0 cos ωt dalam jangka pendek d dan tidak
memperhatikan diri sendiri saat ini dengan pemutusan semu pada setiap ujung.
GAMBAR
14.17
Sebuah
filamen arus diferensial panjang d membawa arus
Kita tidak harus mencoba pada saat ini untuk menemukan
"sumber dari sumber," tetapi hanya akan berasumsi bahwa distribusi
saat ini tidak dapat diubah oleh bidang apa pun yang dihasilkannya.
Langkah
pertama adalah penerapan ekspresi potensi magnet vektor terbelakang, seperti
yang disajikan dalam Sec. 10,5,
di mana [I] adalah fungsi dari waktu
terbelakang t — R/v. Ketika satu frekuensi digunakan untuk menggerakkan antena,
v adalah kecepatan fase pada frekuensi tersebut. Karena tidak ada integrasi
yang diperlukan untuk filamen pendek yang diasumsikan, kita memiliki
Hanya komponen z dari A yang ada, untuk
arus hanya dalam arah a_Z. Pada titik P
mana pun , jauh R dari asal, potensi vektor terhambat oleh R / v dan
menjadi
demikian
GAMBAR
14.18
Resolusi
ke dalam dua komponen sferis Sketsa ditarik sewenang-wenang pesawat
Hanya dengan mengambil sebagian turunan yang di indikasikan.
Demikian
dan
Komponen-komponen medan listrik
yang harus dikaitkan dengan medan magnet ini ditemukan dari bentuk titik hukum peredaran
Ampere karena berlaku untuk daerah di mana konduksi dan konveksi arus tidak
ada,
Atau pada notasi yang rumit
Perluasan dari kerut pada koordinat bola mengarah pada
atau
ntuk
menyederhanakan penafsiran istilah-istilah yang diapit dalam tanda kurung di
atas, kami membuat substitusi menghasilkan :
Ketiga persamaan ini menunjukkan
alasan bahwa begitu banyak masalah yang melibatkan antena diselesaikan dengan
metode eksperimental daripada teoritis. Mereka dihasilkan dari tiga langkah
umum: integrasi (tidak lazim) dan dua diferensiasi. Langkah-langkah ini cukup
untuk menyebabkan elemen arus sederhana dan ekspresi arus sederhana untuk
"meledak" ke dalam medan rumit yang dijelaskan oleh (81) ke (83).
Terlepas dari kerumitan ini, beberapa pengamatan yang menarik dimungkinkan.
Mengetahui
bahwa cos(a-b)= cos a cos b + sin a sin b Kita dapat menyederhanakan hasil ini menjadi
Amplitudo instan dari H_θ
untuk kasus khusus dari elemen saat ini I_0
d=4π. dan λ=1 diplot di θ=90° dan t = 0 (a) di wilayah 1 ≤ r ≤ 2 dekat dengan antena, dan (b) pada wilayah 101
≤ r ≤ 102jauh dari antena. Kurva kiri terasa nonsinusoidal, karena jika itu
adalah sinusoid, titik akhirnya harus mencapai sumbu r tepat pada 1 dan 2.
dalam ekspresi E_θS hampir mencapai 250, 16, dan 1, masing-masing,
ketika r adalah 1 cm. Variasi medan listrik sebagai 1/r^3 harus mengingatkan kita tentang medan
elektrostatik dari dipol (Chap. 4). Istilah ini merepresentasikan energi yang
tersimpan dalam bidang reaktif (kapasitif), dan itu tidak berkontribusi pada
kekuatan yang terpancar. Istilah kuadrat terbalik dalam ekspresi H_ϕs sama pentingnya hanya di wilayah yang sangat
dekat dengan elemen saat ini dan sesuai dengan bidang induksi elemen dc yang
diberikan oleh hukum Biot-Savart. Pada jarak yang sesuai dengan 10 atau lebih
panjang gelombang dari elemen arus berosilasi, semua istilah kecuali jarak
inverse (1 / r) mungkin diabaikan dan medan jauh atau radiasi menjadi
atau
Hubungan antara E_θs dan H_ϕs dengan demikian terlihat bahwa antara medan
listrik dan medan magnet dari gelombang bidang yang seragam, sehingga
memperkuat kesimpulan yang kita capai ketika menyelidiki panjang gelombang.
Variasi kedua medan radiasi dengan sudut kutub 0
adalah sama; bidang maksimum di bidang ekuatorial (bidang xy) dari elemen saat
ini dan menghilang dari ujung elemen. Variasi dengan sudut dapat ditunjukkan
dengan memplot pola vertikal (dengan asumsi orientasi vertikal dari elemen saat
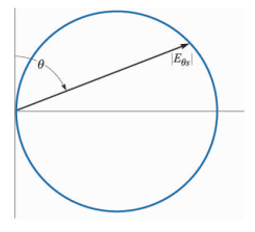
ini) di mana besarnya relatif E_θs diplot terhadap 0 untuk r konstan. Pola ini
biasanya ditunjukkan pada koordinat kutub, seperti pada Gambar 14.20. Pola
horizontal juga dapat diplot untuk sistem antena yang lebih rumit dan
menunjukkan variasi intensitas medan dengan ϕ. Pola horizontal elemen saat ini
adalah lingkaran yang berpusat pada titik asal karena bidang bukan merupakan
fungsi sudut azimuth.
Untuk mendapatkan ekspresi kuantitatif untuk daya
yang dipancarkan, kita perlu menerapkan vektor Poynting ρ = E x H dikembangkan
di Sec. 11.3. Ekspresi instan untuk komponen radiasi dari intensitas medan
listrik dan magnet adalah
GAMBAR
14,20
Plot
polar dari pola vertikal dari elemen arus vertikal. Amplitudo puncak diplot
sebagai fungsi dari sudut kutub pada jarak r konstan. Lokus adalah sebuah
lingkaran.
dan dengan demikian
Kekuatan total (dalam ruang)
seketika (dalam waktu) melintasi permukaan suatu bola lingkup adalah kemudian
Dan
daya waktu rata-rata diberikan oleh setengah amplitudo maksimum
Dimana
η=120πΩ di ruang bebas..
Ini
adalah kekuatan yang sama dengan kekuatan yang akan dihilangkan dalam sebuah perlawanan
R_rad oleh I_0 saat ini ketika tidak ada radiasi apapun,
dimana
GAMBAR
14.21
Antena pendek () memiliki distribusi arus linier
dan dapat didorong oleh saluran dua kawat
titik umpan kecil dan memiliki efek yang
dapat diabaikan. Antena simetris dari jenis ini disebut dipol. Variasi arus
linier dengan jarak adalah asumsi yang masuk akal untuk antena yang memiliki
panjang keseluruhan kurang dari sekitar seperempat panjang gelombang.
Adalah mungkin untuk memperluas analisis dari elemen
arus diferensial ke dipol pendek jika kita mengasumsikan bahwa panjangnya cukup
pendek sehingga efek retardasi dapat diabaikan. Artinya, kami menganggap bahwa
sinyal yang tiba di setiap titik bidang P dari dua ujung antena berada dalam
fase. Arus rata-rata di sepanjang antena adalah I_0/2, dimana I_0 adalah arus input pada terminal pusat. Dengan
demikian, intensitas medan listrik dan magnet akan menjadi setengah nilai yang
diberikan dalam (84) dan (85), dan tidak ada perubahan dalam pola vertikal dan
horizontal. Kekuatan akan menjadi seperempat dari nilai sebelumnya, dan dengan
demikian resistensi radiasi juga akan menjadi seperempat dari nilai yang
diberikan oleh (86).
Jika kita mencoba untuk
meningkatkan hasil kita dengan mengasumsikan variasi sinusoidal dari
amplitudo
saat ini dengan jarak sepanjang antena, dan jika efek keterbelakangan
dimasukkan dalam analisis, maka integrasi yang diperlukan untuk menemukan A dan
kekuatan yang diradiasikan menjadi jauh lebih sulit. Karena kami ingin bergegas
menuju halaman terakhir, mari kita catat bahwa untuk antena paling populer di
dunia, dipol setengah gelombang (d < λ/2), hasil berikut akhirnya diperoleh
FIGURE 14.22
(a) Monopi yang ideal selalu dikaitkan dengan pesawat yang
sempurna. (B) Monopole ditambah gambarnya membentuk dipol.
D14.8.
Hitung nilai untuk kurva yang ditunjukkan pada Gambar 14.19a pada r = 1, 1.2,
1.4, 1.6, 1.8, dan 2.
Jawaban. 1.00; 5.19; 2.23; —2.62;
—3.22; 0.25.
D14.9. Sebuah antena pendek dengan
distribusi arus seragam di udara I_0 d=3×〖10〗^(-4)
A⋅dan m
dan λ=10cm. Temukan |E_θS |pada θ=90°, ϕ=0°, dan r=;(a) 2 cm; (b) 20 cm; (c)
200 cm.
Jawaban. 24.8 V/m; 2.82 V/m; 0.283 V/m.
D14.10. Antena monopole Gambar. 14.22a memiliki panjang d/2 = 0.080
m dan dapat diasumsikan membawa distribusi arus segitiga untuk arus umpan I_0 adalah 16.0 A pada frekuensi 375
Bintang Dwi Egatara ( 07 / TT2B )
Risca Erfian Rahmadani (19 / TT2B)
Deni Arifani Nafis ( 9 / TT2B)